Definition and Types of Cones
– A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.
– A cone can be formed by connecting a common point (the apex) to all the points on a base.
– The base of a cone can be a circle, any one-dimensional quadratic form, or any closed one-dimensional figure.
– If the enclosed points are included in the base, the cone is a solid object; otherwise, it is a two-dimensional object.
– Cones can be right circular, oblique, double, or truncated.
– A truncated cone is a cone with a region including its apex cut off by a plane.
Measurements and Equations
– The volume of a conic solid is one third of the product of the base area and the height.
– The center of mass of a conic solid lies one-quarter of the way from the center of the base to the vertex.
– For a circular cone, the volume is one third of the product of the base area and the height.
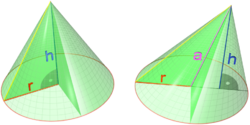
– The slant height of a right circular cone is the distance from any point on the base circle to the apex.
– The lateral surface area of a right circular cone is the product of pi, the radius, and the slant height.
Right Circular Cone
– The volume of a right circular cone is one third of the product of pi, the square of the radius, and the height.
– The slant height of a right circular cone is given by the square root of the sum of the square of the radius and the square of the height.
– The lateral surface area of a right circular cone is the product of pi, the radius, and the slant height.
– The total surface area of a right circular cone is the sum of the lateral surface area and the area of the base.
– The surface area of the base circle of a cone is equal to pi times the square of the radius.
Other Types of Cones
– An elliptical cone has an elliptical base.
– A generalized cone is the surface created by the set of lines passing through a vertex and every point on a boundary.
– Cones can also be generalized to higher dimensions.
– Depending on the context, cone may also mean specifically a convex cone or a projective cone.
– A cone with a polygonal base is called a pyramid.
Projective Geometry and Generalizations
– In projective geometry, a cylinder is a cone whose apex is at infinity.
– Taking the limit as the apex goes to infinity, one obtains a cylinder.
– The angle of the side of the cylinder increases as arctan, forming a right angle in the limit.
– Cylindrical conics are used in the definition of degenerate conics.
– The definition of a cone can be extended to higher dimensions.
– A convex set in a real vector space is a cone if every vector multiplied by a nonnegative real number is also in the set.
– Polyhedral cones are often of interest in this context.
– Topological cones can be defined in arbitrary topological spaces.
– Circular cones are not usually special in higher dimensions. Source: https://en.wikipedia.org/wiki/Cone_(geometry)
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex.
| Cone | |
|---|---|
 A right circular cone with the radius of its base r, its height h, its slant height c and its angle θ. | |
| Type | Solid figure |
| Faces | 1 circular face and 1 conic surface |
| Euler char. | 2 |
| Symmetry group | O(2) |
| Surface area | πr2 + πrℓ |
| Volume | (πr2h)/3 |


A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the lateral surface; if the lateral surface is unbounded, it is a conical surface.
In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a double cone. Either half of a double cone on one side of the apex is called a nappe.
The axis of a cone is the straight line (if any), passing through the apex, about which the base (and the whole cone) has a circular symmetry.
In common usage in elementary geometry, cones are assumed to be right circular, where circular means that the base is a circle and right means that the axis passes through the centre of the base at right angles to its plane. If the cone is right circular the intersection of a plane with the lateral surface is a conic section. In general, however, the base may be any shape and the apex may lie anywhere (though it is usually assumed that the base is bounded and therefore has finite area, and that the apex lies outside the plane of the base). Contrasted with right cones are oblique cones, in which the axis passes through the centre of the base non-perpendicularly.

A cone with a polygonal base is called a pyramid.
Depending on the context, "cone" may also mean specifically a convex cone or a projective cone.
Cones can also be generalized to higher dimensions.
