Complex number

Definition and Representation of Complex Numbers
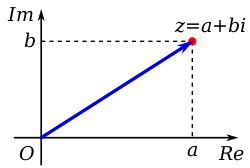
– A complex number is a number of the form a + bi, where a and b are real numbers and i is the imaginary unit.
– Complex numbers can be added and multiplied using the addition and multiplication for polynomials.
– The real part of a complex number is denoted as Re(z), while the imaginary part is denoted as Im(z).
– Complex numbers can be expressed in Cartesian or algebraic form, where the real part is represented on the horizontal axis and the imaginary part on the vertical axis.
– The set of all complex numbers is denoted by C or �.
– Complex numbers can be represented as ordered pairs (a, b) or as coordinates of a point in a two-dimensional space.
– The complex plane, also known as the Argand diagram, is a common way to visualize complex numbers.
– The Cartesian complex plane uses horizontal and vertical axes to represent the real and imaginary parts, respectively.
– Another visualization option is the polar coordinate system, which uses the distance from the origin and the angle to locate a point in the complex plane.
– The Riemann sphere is a two-dimensional surface of a sphere where the coordinates of a complex number can be projected.

Polar Complex Plane and Modulus and Argument
– The polar coordinate system is an alternative option for representing complex numbers in the complex plane.
– It uses the distance from the origin (modulus) and the angle subtended between the positive real axis (argument) to locate a point.
– The modulus and argument of a complex number determine its position in the polar complex plane.
– The polar form of a complex number is expressed as r(cos(φ) + i sin(φ)), where r is the modulus and φ is the argument.
– The polar complex plane is useful for understanding multiplication and exponentiation of complex numbers.
– The modulus of a complex number represents its distance from the origin in the polar complex plane.
– The argument of a complex number represents the angle it forms with the positive real axis in the polar complex plane.
– The modulus and argument together uniquely determine a complex number in the polar form.
– The modulus of a complex number z is denoted as |z|, while the argument is denoted as arg(z) or φ.
– The polar form of a complex number allows for easier multiplication and exponentiation operations.

Visualization of Complex Functions
– Complex functions require both a complex input and output.
– Visualizing complex functions in a four-dimensional space is not possible, so alternative methods have been developed.
– Domain coloring is a visualization technique where color and brightness represent the argument and magnitude of complex numbers, respectively.
– Dark spots on a color wheel graph indicate moduli near zero, while brighter spots indicate points farther away from the origin.
– Color wheel graphs provide a simple way to visualize complex functions without losing information.

History and Contributions of Mathematicians
– Complex numbers were conceived in the 16th century by mathematicians like Gerolamo Cardano and Niccolò Fontana Tartaglia.
– The use of complex numbers became necessary when solving cubic and quartic polynomials, even if only real solutions were sought.
– Rafael Bombelli developed rules for complex arithmetic to address the paradoxical solutions of cubic equations.
– René Descartes coined the term ‘imaginary’ for complex numbers to emphasize their unreal nature.
– The use of the symbol ‘i’ to represent the square root of -1 was introduced to avoid inconsistencies in algebraic calculations.
– Italian mathematician Rafael Bombelli developed rules for complex arithmetic.
– Irish mathematician William Rowan Hamilton introduced a more abstract formalism for complex numbers and extended it to quaternions.
– Italian mathematicians Niccolò Fontana Tartaglia and Gerolamo Cardano discovered algebraic solutions for cubic and quartic polynomials.
– Greek mathematician Hero of Alexandria made a fleeting reference to square roots of negative numbers in his work.
– Leonhard Euler encountered difficulties with the use of square roots of negative numbers in complex number calculations.

Application and Importance of Complex Numbers
– Complex numbers are used in various fields, including physics, engineering, and mathematics.
– They are essential in solving problems involving alternating current (AC) circuits.
– Complex numbers provide a complete and algebraically closed field, ensuring that every polynomial equation has a root.
– The fundamental theorem of algebra guarantees the existence of a solution to every polynomial equation of degree one or higher.
– Complex numbers allow for a deeper understanding and analysis of mathematical concepts and phenomena.
– In network analysis of electrical circuits, the complex conjugate is used to find the impedance of a circuit.
– Complex analysis, initiated by Cauchy and Riemann, brought fundamental ideas to completion in the 19th century. Source:  https://en.wikipedia.org/wiki/Complex_number

Complex number (Wikipedia)

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Complex number" – news · newspapers · books · scholar · JSTOR (July 2022) (Learn how and when to remove this template message)

In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted i, called the imaginary unit and satisfying the equation ${\displaystyle i^{2}=-1}$; every complex number can be expressed in the form ${\displaystyle a+bi}$, where a and b are real numbers. Because no real number satisfies the above equation, i was called an imaginary number by René Descartes. For the complex number ${\displaystyle a+bi}$, a is called the real part, and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols ${\displaystyle \mathbb {C} }$ or C. Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world.

Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficients has a solution which is a complex number. For example, the equation ${\displaystyle (x+1)^{2}=-9}$ has no real solution, since the square of a real number cannot be negative, but has the two nonreal complex solutions ${\displaystyle -1+3i}$ and ${\displaystyle -1-3i}$.

Addition, subtraction and multiplication of complex numbers can be naturally defined by using the rule ${\displaystyle i^{2}=-1}$ combined with the associative, commutative, and distributive laws. Every nonzero complex number has a multiplicative inverse. This makes the complex numbers a field that has the real numbers as a subfield. The complex numbers also form a real vector space of dimension two, with {1, i} as a standard basis.

This standard basis makes the complex numbers a Cartesian plane, called the complex plane. This allows a geometric interpretation of the complex numbers and their operations, and conversely expressing in terms of complex numbers some geometric properties and constructions. For example, the real numbers form the real line which is identified to the horizontal axis of the complex plane. The complex numbers of absolute value one form the unit circle. The addition of a complex number is a translation in the complex plane, and the multiplication by a complex number is a similarity centered at the origin. The complex conjugation is the reflection symmetry with respect to the real axis. The complex absolute value is a Euclidean norm.

In summary, the complex numbers form a rich structure that is simultaneously an algebraically closed field, a commutative algebra over the reals, and a Euclidean vector space of dimension two.