Angular Frequency in Circular Motion
– Circular motion involves objects rotating or orbiting around an axis.
– The distance from the axis (r), tangential speed (v), and angular frequency (ω) are related in circular motion.
– During one period (T), a body in circular motion travels a distance equal to the circumference of the path traced out by the body (2πr).
– The angular frequency (ω) can be calculated using the equation ω = v/r.
– The mass of the object does not affect the angular frequency in circular motion.
Angular Frequency in LC Circuits
– LC circuits consist of a combination of inductance (L) and capacitance (C) elements.
– The resonant angular frequency (ω) in a series LC circuit is determined by the square root of the reciprocal of the product of the capacitance and inductance (ω = √(1/LC)).
– Adding series resistance does not change the resonant frequency of a series LC circuit.
– For parallel tuned circuits, the resonant frequency depends on the losses of parallel elements.
– LC circuits are commonly used in electronic devices such as filters and oscillators.
Terminology and Distinction
– Angular frequency is often referred to as frequency, but it differs from frequency by a factor of 2π.
– This distinction can lead to confusion when the terms are used interchangeably.
– Frequency measures the number of cycles or oscillations per unit of time, while angular frequency measures the rate of change of angular displacement.
– Angular frequency is measured in radians per second (rad/s), while frequency is measured in hertz (Hz).
– It is important to use the appropriate term depending on the context to avoid misunderstandings.
Related Concepts
– Cycle per second: Another term for frequency, representing the number of cycles or oscillations per second.
– Radian per second: The unit of measurement for angular frequency, representing the rate of change of angular displacement.
– Degree (angle): A unit of measurement for angles, where a full circle is divided into 360 degrees.
– Mean motion: The average angular velocity or frequency of an object in motion.
– Orders of magnitude (angular velocity): A way to express the magnitude of angular velocity using powers of ten, allowing for easy comparison of different values.
– Rotational frequency: The number of rotations per unit of time, often used in the context of rotating objects or systems.
– Simple harmonic motion: A type of periodic motion where the acceleration of an object is directly proportional to its displacement and opposite in direction.
– These concepts are closely related to angular frequency and provide a broader understanding of rotational and oscillatory motion.
Examples and Applications
– Circular motion: In a rotating or orbiting object, there is a relationship between the distance from the axis (r), tangential speed (v), and angular frequency (ω).
– LC circuits: In a series LC circuit, the resonant angular frequency (ω) is equal to the square root of the reciprocal of the product of the capacitance (C) and the inductance (L) of the circuit.
– Oscillation: When an object oscillates, its acceleration can be calculated using the equation a = -ω^2x, where ω is the angular frequency and x is the displacement from an equilibrium position.
– Harmonic motion: Angular frequency is closely related to the concept of simple harmonic motion, where the acceleration of an object is directly proportional to its displacement and opposite in direction. Source: https://en.wikipedia.org/wiki/Angular_frequency
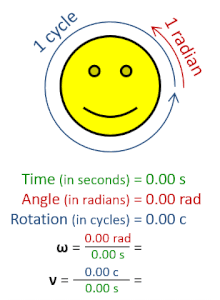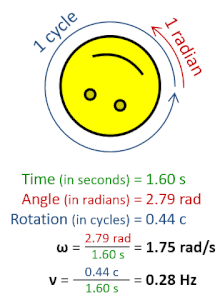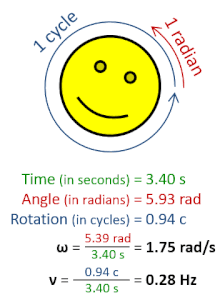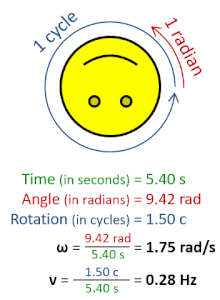
In physics, angular frequency (symbol ω), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine function (for example, in oscillations and waves). Angular frequency (or angular speed) is the magnitude of the pseudovector quantity angular velocity.
| Angular frequency | |
|---|---|
 | |
Other names | angular speed, angular rate |
Common symbols | ω |
| SI unit | radians per second (rad/s) |
Other units | degrees per second (°/s) |
| In SI base units | s-1 |
Derivations from other quantities | ω=2π rad ⋅ ν, ω=dθ/dt |
| Dimension | |

Angular frequency can be obtained multiplying rotational frequency, ν (or ordinary frequency, f) by a full turn (2π radians): ω=2π rad ⋅ ν. It can also be formulated as ω=dθ/dt, the instantaneous rate of change of the angular displacement, θ, with respect to time, t.

